DFS和BFS

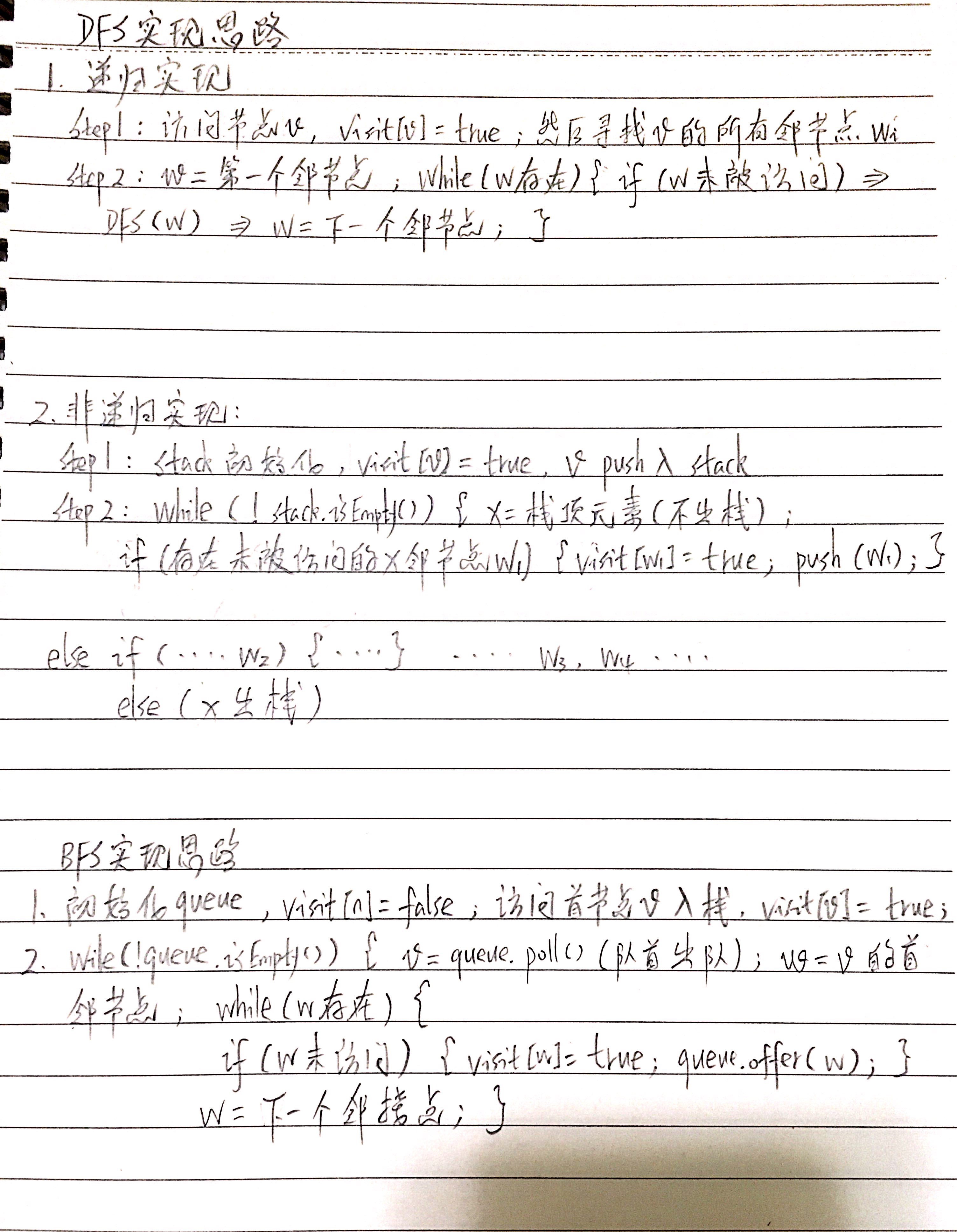
Tree

1. 二叉查找树:（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；（3）左、右子树也分别为二叉排序树；（4）没有键值相等的结点 (5) 特性就是”中序遍历“可以让结点有序.

   • 范围查找是我们使用二叉树的最终目的，既然是范围查找，我们就知道了一个”min“和”max“，其实实现起来也很简单：
   • 我们要在树中找到min元素，当然min元素可能不存在，但是我们可以找到min的上界，耗费时间为O(logn)
   • 从min开始我们中序遍历寻找max的下界。耗费时间为m。m也就是匹配到的个数

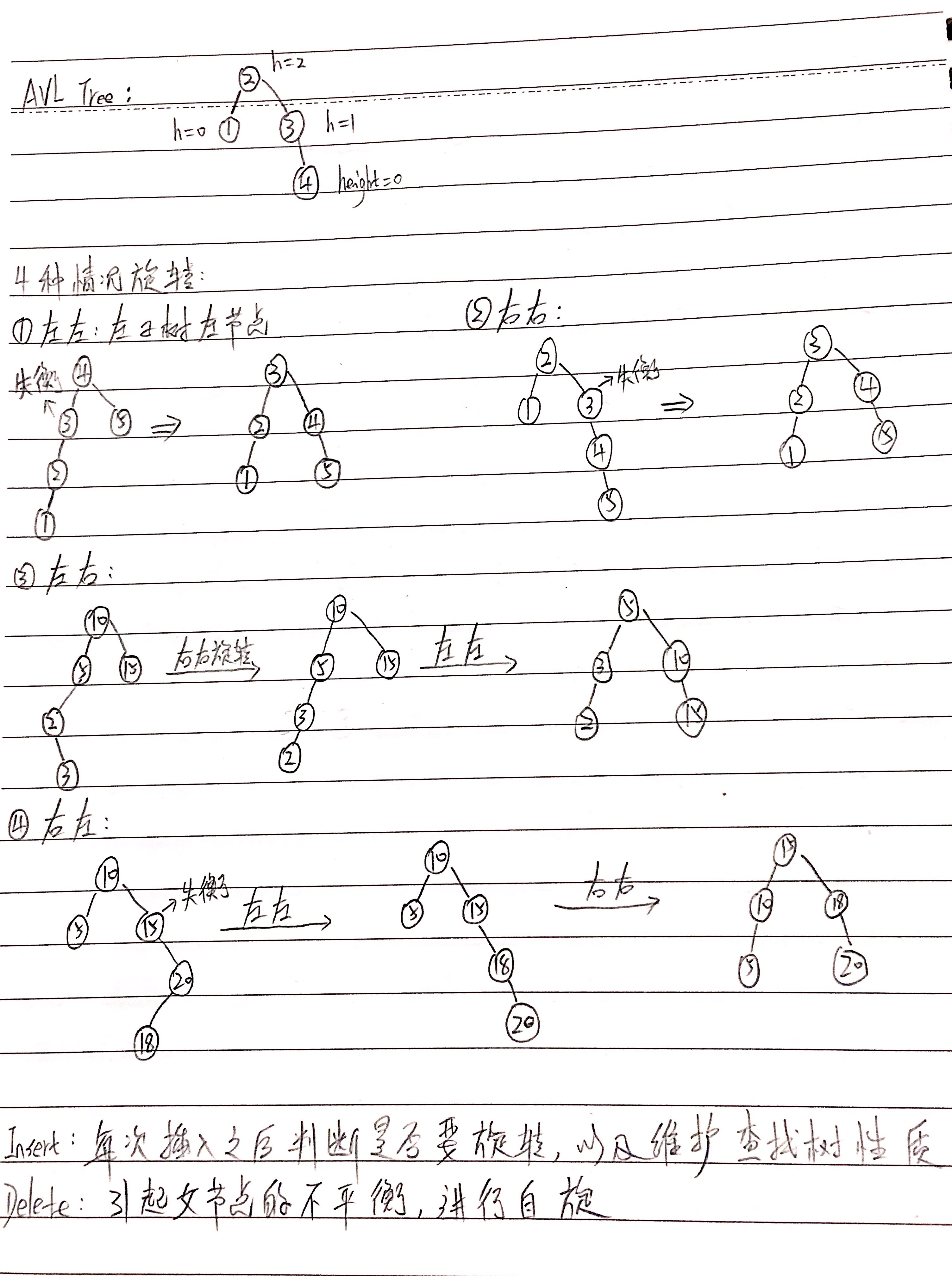
2. 平衡二叉查找树(AVL): 父节点的左子树和右子树的高度之差不能大于1的二叉查找树，平衡之后能够保证查找，添加，删除的平均和最差时间复杂度都是严格的O(logN) Link

   

3. B-Tree:
   

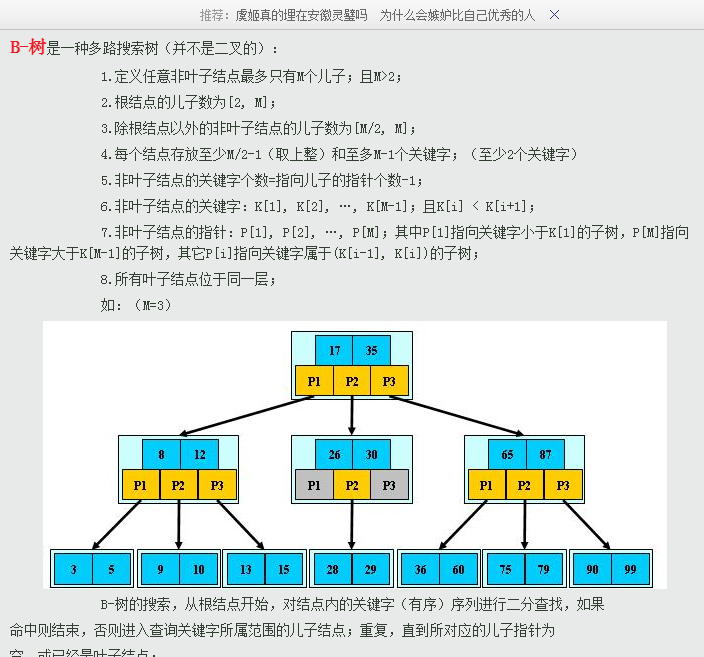
4. B+ Tree:一棵m阶的B+树和m阶的B树的异同点在于：
   • 所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。(而B 树的叶子节点并没有包括全部需要查找的信息)
   • 所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。(而B 树的非终节点也包含需要查找的有效信息)
5. 为什么说B+树比B 树更适合实际应用中操作系统的文件索引和数据库索引？
   • B+树的磁盘读写代价更低：B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。
   • B+树的查询效率更加稳定：由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

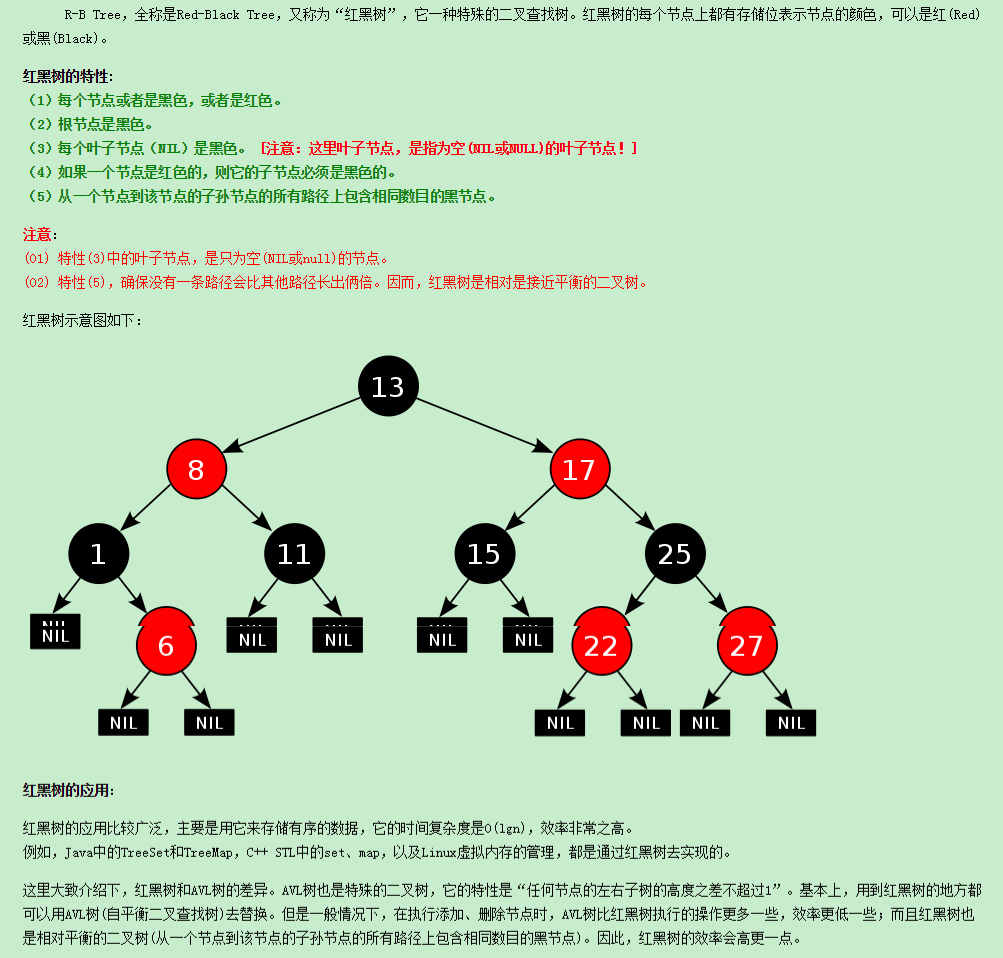
6. RB-Tree红黑树:
   

7. 为什么MySQL数据库要用B+树存储索引？而不是B tree或者hashTable

   KNN算法

8. 基本思想: 从训练样本中找出K个与其最相近的样本，然后看这K个样本中哪个类别的样本多，则待判定的值（或说抽样）就属于这个类别

9. 步骤:

   • 计算已知类别数据集中每个点与当前点的距离；
   • 选取与当前点距离最小的K个点；
   • 统计前K个点中每个类别的样本出现的频率；
   • 返回前K个点出现频率最高的类别作为当前点的预测分类

10. 算法关键:Link

11. 优缺点和应用场景

排序算法

插入与冒泡

快排

堆排

归并

o(n)的排序算法：基数排序+计数排序+通排序

桶排序

1. 适用场景：待排序的元素能够均匀分布在某一个范围[MIN, MAX]之间
2. 空间复杂度是O(n)，因为需要额外的桶和桶内的元素链表空间；一种稳定的排序

决策树算法

神经网络算法

海量数据处理算法

Top K 问题解法

ListView下拉刷新和下拉加载

1. 安装homebrew包管理器

   //卸载brew命令
   ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/uninstall)"
   
   //安装 brew命令
   /usr/bin/ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)"
   

2. Install Android SDK and NDK by run brew install android-ndk android-sdk

3. 设置sdk全局变量和NDK全局变量,在~目录下新建或打开.bash_profile文件，添加两行export命令引入ndk和sdk文件夹,再在terminal执行source .bash_profile

   export ANDROID_HOME=~/sdk            
   export ANDROID_NDK_HOME=~/ndk/android-ndk-r10e 
   

4. cd 进入sdk目录下tools子目录,运行两个命令更新sdk

   echo "y" | ./android update sdk --filter tools,platform-tools,build-tools-23.0.2,android-23,extra-google-m2repository --no-ui -a
   
   echo "y" | ./android update sdk --filter extra-android-m2repository --no-ui --no-https -a
   

5. cd进入shadowsocks-android目录执行

   1	6. 安装sbt：``` brew install sbt

6. 生成keystore文件和Create local.properties from local.properties.example

   keytool -genkey -v -keystore release.keystore -alias release -keyalg RSA -keysize 2048 -validity 10000
   

7. sbt编译

   // Build native binaries
   ./build.sh
   
   // Build the apk
   sbt clean android:package-release
   

BitSet位图

1. BitSet原理BitSet位图类实现了一个按需增长的位向量，每一位值只有0或1，可以用1位来表示一个数据是否出现过，0为没有出现过，1表示出现过；内部维护了一个long数组，初始只有一个long，所以BitSet最小的size是64，当随着存储的元素越来越多，BitSet内部会动态扩充，最终内部是由N个long来存储。
2. 常见的应用是那些需要对海量数据进行一些统计工作的时候，比如日志分析等；一个1G的空间有 8102410241024=8.5810^9bit，也就是可以表示85亿个不同的数
3. 问题1：现在有1千万个随机数，随机数的范围在1到1亿之间。将1到1亿之间没有在随机数中的数求出来；问题2：两个10G文本, 里边是1-1亿的数字，怎么找出一个里边没有的3个数？答案：如果有足够的内存的话可以用位图法，即开一个1亿位的bitset，内存为100m/8== 12.5m, 然后如果一个数有出现，对应的bitset上标记为1，最后统计bitset上为0的即可。

链表相关问题

1. 在O(1)时间删除链表节点
2. 单链表的转置
3. 求链表倒数第k个节点
4. 求链表的中间节点
5. 判断单链表是否存在环
6. 找到环的入口点
7. 编程判断两个链表是否相交
8. 扩展：链表有环，如何判断相交
9. 扩展：两链表相交的第一个公共节点

求二叉树的深度(从根节点到叶子结点一次经过的结点形成树的一条路径，最长路径的长度为树的深度。根节点的深度为1。)

private static int getTreeHeight(TreeNode root) {
    if (root == null)
        return 0;
    // 左子树depth与右子树depth的较大值+1即为tree的depth
    int left = getTreeHeight(root.left);
    int right = getTreeHeight(root.right);

    return left>right ? left+1:right+1;
}

求二叉树的节点个数

求二叉树第K层的节点个数

private static int kLevelNodeNumber(TreeNode root, int k) {
    // 第k层节点数可以看做是左子树的k-1层节点数+右子树的k-1层节点数
    if (root == null || k <= 0)
        return 0;
    if (k == 1)
        return 1;
    int leftNodeNum = kLevelNodeNumber(root.left, k-1);
    int rightNodeNum = kLevelNodeNumber(root.right, k-1);

    return leftNodeNum+rightNodeNum;
}

求二叉树中叶子节点的个数

private static int leafNodeNumber(TreeNode root) {
    if (root == null)
        return 0;
    if (root.left == null && root.right == null)
        return 1;
    return leafNodeNumber(root.left) + leafNodeNumber(root.right);

}

反转二叉树(求二叉树镜像) —- 递归和循环解法

判断两棵二叉树是否结构相同

private static boolean EqualsOrNot(TreeNode node1, TreeNode node2) {
    // 如果两棵二叉树都为空，返回真;一真一假则返回false
    if (node1 == null && node2 == null) 
        return true;
    else if(node1==null || node2==null)
        return false;
    boolean left = EqualsOrNot(node1.left, node2.left);
    boolean right = EqualsOrNot(node1.right, node2.right);
    // 如果对应的左子树和右子树都为true则返回真
    return left && right;
}

判断一个二叉树是否是完全二叉树

完全二叉树：二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边
思路：任意的一个二叉树，都可以补成一个满二叉树。这样中间就会有很多空洞。在广度优先遍历的时候，如果是满二叉树，或者完全二叉树，这些空洞是在广度优先的遍历的末尾，当我们遍历到空洞的时候，整个二叉树就已经遍历完成了。而如果遍历到空洞还没有完成遍历则说明它是非完全二叉树

private static boolean isCompleteBT(TreeNode root) {

    LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
    // 进行广度优先遍历（层次遍历），并把NULL节点也放入队列
    TreeNode node;
    queue.offer(root);
    while((node=queue.poll()) != null) {
        queue.offer(node.left);
        queue.offer(node.right);
    }
    // 有未访问到的的非NULL节点，则树存在空洞，为非完全二叉树
    while(!queue.isEmpty()) {
        if (queue.poll() != null)
            return false;
    }
    return true;
}

判断二叉树是不是平衡二叉树

平衡二叉树它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

private static int getTreeHeight(TreeNode root) {
    if (root == null)
        return 0;
    // 左子树depth与右子树depth的较大值+1即为tree的depth
    int left = getTreeHeight(root.left);
    int right = getTreeHeight(root.right);

    return left>right ? left+1:right+1;
}

private static boolean isBalanceBT(TreeNode root) {
    if (root == null)
        return true;
    int leftHeight = getTreeHeight(root.left);
    int rightHeight = getTreeHeight(root.right);
    // 左右子树的高度之差应该<=1;而且左右子树都应该是平衡二叉树
    if (Math.abs(leftHeight-rightHeight) > 1)
        return false;
    else
        return isBalanceBT(root.left) && isBalanceBT(root.right);
}

优化解法: 只后序遍历二叉树一次，一边遍历一边比较左右子树的深度差

判断二叉树B是不是A的子结构

思路: 第一步在树A中找到和B的根节点的值一样的节点R，第二步再判断A中以R为根节点的子树是不是包含和树B一样的结构

private boolean isBsubTreeOfA(TreeNode rootA, TreeNode rootB) {
    boolean res = false;
    if (rootA != null && rootB != null) {
        if (rootA.val == rootB.val)
            res = EqualsTreeOrNot.EqualsOrNot(rootA, rootB);// 判断两棵树是否结构相同
        if (!res)
            res = isBsubTreeOfA(rootA.left, rootB);
        if (!res)
            res = isBsubTreeOfA(rootA.right, rootB);
    }
    return res;
}

求二叉树中两个节点的最低公共祖先节点

// 二叉查找树
public static TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {

    if (root.val > p.val && root.val > q.val)
        return lowestCommonAncestor(root.left, p, q);
    else if (root.val < p.val && root.val < q.val)
        return lowestCommonAncestor(root.right, p, q);
    else
        return root;
}
// 普通树二叉树
public static TreeNode lowestCommonAncestorBT(TreeNode root, TreeNode p, TreeNode q) {
    // 对二叉树做一个前序遍历，如果找到目标节点或者到了叶节点就return,对于return的结果进行判断
    // ，两者都!null说明root就是这两个节点的最近公共父节点;否则返回非空的那一个节点；回溯过程中到达最近公共父节点时会满足两者都!null
    if (root == null || root == p || root == q)
        return root;
    TreeNode leftNode = lowestCommonAncestorBT(root.left, p, q);
    TreeNode rightNode = lowestCommonAncestorBT(root.right, p, q);
    if (leftNode != null && rightNode != null) {
        return root;
    } else if (leftNode != null) {
        return leftNode;
    } else {
        return rightNode;
    }
}

求二叉树中两个节点之间的最大距离

private static int getTreeHeight(TreeNode root) {
    if (root == null)
        return 0;
    // 左子树depth与右子树depth的较大值+1即为tree的depth
    int left = getTreeHeight(root.left);
    int right = getTreeHeight(root.right);

    return left>right ? left+1:right+1;
}

private static int findMaxDistance(TreeNode root) {
    if (root == null)
        return 0;
    // 左右子树中的最大距离
    int leftMaxDis = findMaxDistance(root.left);
    int rightMaxDis = findMaxDistance(root.right);

    // 左右子树的最大Height
    int leftHeight = 0, rightHeight = 0;
    if (root.left != null)
        leftHeight = getTreeHeight(root.left);
    if (root.right != null)
        rightHeight = getTreeHeight(root.right);

    int max = leftMaxDis > rightMaxDis ? leftMaxDis : rightMaxDis;
    return max>(leftHeight+rightHeight) ? max:(leftHeight+rightHeight);
}

将二叉查找树变为有序的双向链表

思路:将tree看做左子树，根节点，右子树三个部分，然后利用中序遍历先对左子树转变为双向链表然后连接根节点；然后将右子树转变为双向链表，根节点连接到该双向链表；最后返回一个有序双向链表的头结点

private static TreeNode BST2List(TreeNode root) {
    TreeNode lastNodeOfList = null;
    lastNodeOfList = convert(root, lastNodeOfList);
    // 将lastNodeOfList从双向链表尾部移动到头部
    while (lastNodeOfList != null && lastNodeOfList.left != null) {
        lastNodeOfList = lastNodeOfList.left;
    }
    return lastNodeOfList;
}

private static TreeNode convert(TreeNode root, TreeNode lastNodeOfList) {
    if (root == null) {
        return root;
    }
    // 转变左子树为双向链表
    if (root.left != null)
        lastNodeOfList = convert(root.left, lastNodeOfList);
    // 修改双链表尾节点为当前节点
    if (lastNodeOfList != null) {
        root.left = lastNodeOfList;
        lastNodeOfList.right = root;
    }
    lastNodeOfList = root;
    // 转变右子树为双向链表
    if (root.right != null)
        lastNodeOfList = convert(root.right, lastNodeOfList);
    // 返回值为双链表尾节点
    return lastNodeOfList;
}

由前序遍历序列和中序遍历序列重建二叉树

二叉树前序遍历序列中，第一个元素总是树的根节点的值。中序遍历序列中，左子树的节点的值位于根节点的值的左边，右子树的节点的值位于根节点的值的右边。
递归解法：

1. 如果前序遍历为空或中序遍历为空或节点个数小于等于0，返回NULL。
2. 创建根节点。前序遍历的第一个数据就是根节点的数据，在中序遍历中找到根节点的位置，可分别得知左子树和右子树的前序和中序遍历序列，重建左右子树。

二叉树的下一个节点(给定一个二叉树和其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点left和right，同时包含指向父结点的指针next)

思路: 三种情况

1. 如果一个结点有右子树，那么它的下一个结点就是它的右子树中的左子结点。也就是说右子结点出发一直沿着指向左子结点的指针，我们就能找到它的下一个结点。

2. 如果一个结点没有右子树，又可以分为两种情况：

   • 如果结点是它父节点的左子结点，那么它的下一个结点就是它的父结点。

   • 如果一个结点既没有右子树，并且它还是它父结点的右子结点。我们可以沿着指向父节点的指针一直向上遍历，直到找到一个是它父结点的左结点的结点。如果这样的结点存在，那么这个结点的父结点就是我们要找的下一个结点。

     public TreeLinkNode GetNext(TreeNode pNode) {
         TreeNode curNode = null;
         //第一步：判断是否有右孩子
         if(pNode.right != null){
             curNode = pNode.right;
             while(curNode.left != null) curNode = curNode.left;
             return curNode;
         }
         //第二步：判断是否是其父节点的左孩子
         if(pNode.next == null) return null;
         if(pNode == pNode.next.left){
             return pNode.next;
         }
         //第三步：向上找其父节点，直到父节点是其父节点的父节点的左孩子
         curNode = pNode.next;
         while(curNode.next != null){
             if(curNode == curNode.next.left){
                 return curNode.next;
             }
             //继续向上找父节点
             curNode = curNode.next;
         }
         return null;
     }